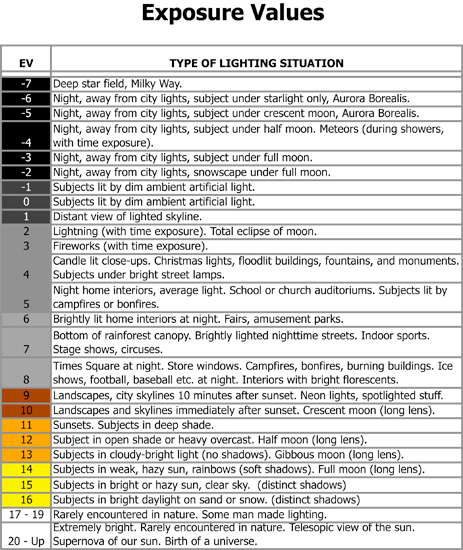
Also see: https://www.pixelsham.com/2015/05/16/how-aperture-shutter-speed-and-iso-affect-your-photos/
In photography, exposure value (EV) is a number that represents a combination of a camera’s shutter speed and f-number, such that all combinations that yield the same exposure have the same EV (for any fixed scene luminance).
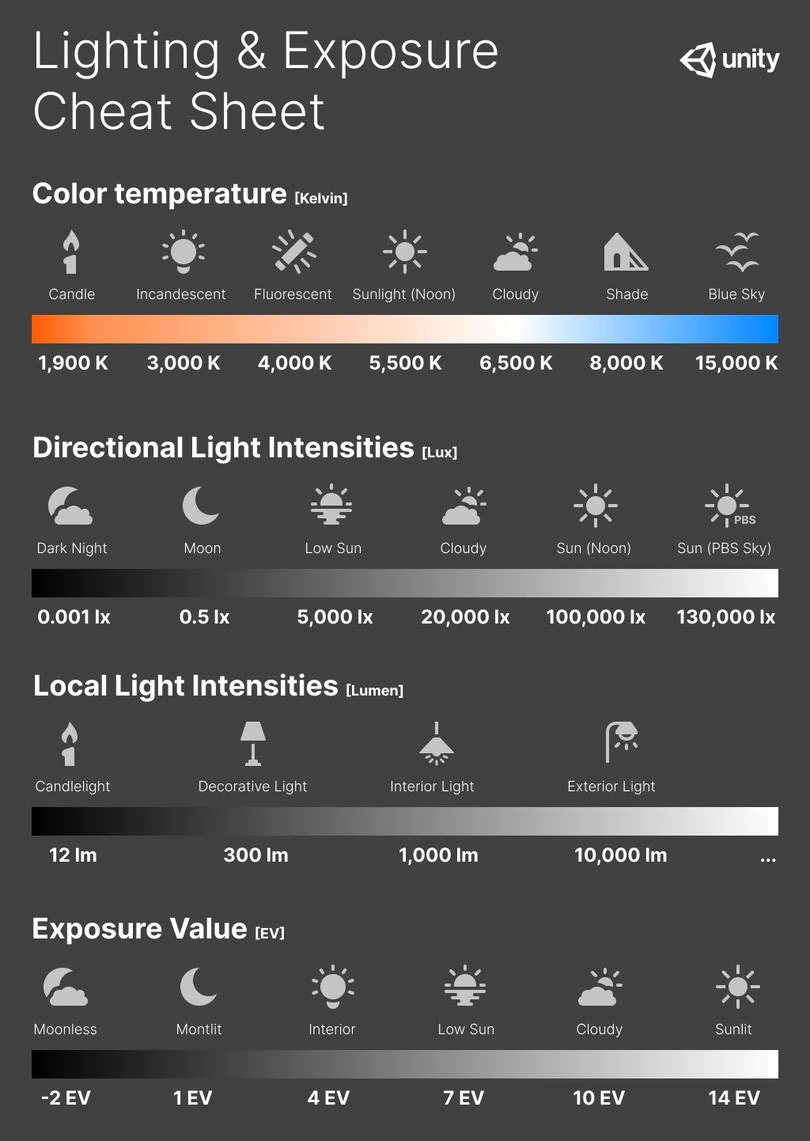
The EV concept was developed in an attempt to simplify choosing among combinations of equivalent camera settings. Although all camera settings with the same EV nominally give the same exposure, they do not necessarily give the same picture. EV is also used to indicate an interval on the photographic exposure scale. 1 EV corresponding to a standard power-of-2 exposure step, commonly referred to as a stop
EV 0 corresponds to an exposure time of 1 sec and a relative aperture of f/1.0. If the EV is known, it can be used to select combinations of exposure time and f-number.
Note EV does not equal to photographic exposure. Photographic Exposure is defined as how much light hits the camera’s sensor. It depends on the camera settings mainly aperture and shutter speed. Exposure value (known as EV) is a number that represents the exposure setting of the camera.
Thus, strictly, EV is not a measure of luminance (indirect or reflected exposure) or illuminance (incidentl exposure); rather, an EV corresponds to a luminance (or illuminance) for which a camera with a given ISO speed would use the indicated EV to obtain the nominally correct exposure. Nonetheless, it is common practice among photographic equipment manufacturers to express luminance in EV for ISO 100 speed, as when specifying metering range or autofocus sensitivity.
The exposure depends on two things: how much light gets through the lenses to the camera’s sensor and for how long the sensor is exposed. The former is a function of the aperture value while the latter is a function of the shutter speed. Exposure value is a number that represents this potential amount of light that could hit the sensor. It is important to understand that exposure value is a measure of how exposed the sensor is to light and not a measure of how much light actually hits the sensor. The exposure value is independent of how lit the scene is. For example a pair of aperture value and shutter speed represents the same exposure value both if the camera is used during a very bright day or during a dark night.
Each exposure value number represents all the possible shutter and aperture settings that result in the same exposure. Although the exposure value is the same for different combinations of aperture values and shutter speeds the resulting photo can be very different (the aperture controls the depth of field while shutter speed controls how much motion is captured).
EV 0.0 is defined as the exposure when setting the aperture to f-number 1.0 and the shutter speed to 1 second. All other exposure values are relative to that number. Exposure values are on a base two logarithmic scale. This means that every single step of EV – plus or minus 1 – represents the exposure (actual light that hits the sensor) being halved or doubled.
Formulas
https://en.wikipedia.org/wiki/Exposure_value
https://www.scantips.com/lights/math.html
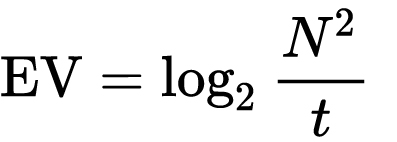
which means 2EV = N² / t
where
- N is the relative aperture (f-number) Important: Note that f/stop values must first be squared in most calculations
- t is the exposure time (shutter speed) in seconds
EV 0 corresponds to an exposure time of 1 sec and an aperture of f/1.0.
Example: If f/16 and 1/4 second, then this is:
(N² / t) = (16 × 16 ÷ 1/4) = (16 × 16 × 4) = 1024.
Log₂(1024) is EV 10. Meaning, 210 = 1024.
Collecting photographic exposure using Light Meters
The exposure meter in the camera does not know whether the subject itself is bright or not. It simply measures the amount of light that comes in, and makes a guess based on that. The camera will aim for 18% gray, meaning if you take a photo of an entirely white surface, and an entirely black surface you should get two identical images which both are gray (at least in theory)
https://en.wikipedia.org/wiki/Light_meter
For reflected-light meters, camera settings are related to ISO speed and subject luminance by the reflected-light exposure equation:
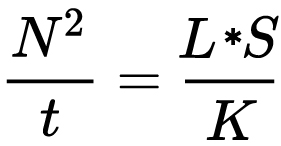
where
- N is the relative aperture (f-number)
- t is the exposure time (“shutter speed”) in seconds
- L is the average scene luminance
- S is the ISO arithmetic speed
- K is the reflected-light meter calibration constant
For incident-light meters, camera settings are related to ISO speed and subject illuminance by the incident-light exposure equation:![]()
where
- E is the illuminance (in lux)
- C is the incident-light meter calibration constant
Two values for K are in common use: 12.5 (Canon, Nikon, and Sekonic) and 14 (Minolta, Kenko, and Pentax); the difference between the two values is approximately 1/6 EV.
For C a value of 250 is commonly used.
Nonetheless, it is common practice among photographic equipment manufacturers to also express luminance in EV for ISO 100 speed. Using K = 12.5, the relationship between EV at ISO 100 and luminance L is then :
L = 2(EV-3)
The situation with incident-light meters is more complicated than that for reflected-light meters, because the calibration constant C depends on the sensor type. Illuminance is measured with a flat sensor; a typical value for C is 250 with illuminance in lux. Using C = 250, the relationship between EV at ISO 100 and illuminance E is then :
E = 2.5 * 2(EV)
https://nofilmschool.com/2018/03/want-easier-and-faster-way-calculate-exposure-formula
Three basic factors go into the exposure formula itself instead: aperture, shutter, and ISO. Plus a light meter calibration constant.
f-stop²/shutter (in seconds) = lux * ISO/C
If you at least know four of those variables, you’ll be able to calculate the missing value.
So, say you want to figure out how much light you’re going to need in order to shoot at a certain f-stop. Well, all you do is plug in your values (you should know the f-stop, ISO, and your light meter calibration constant) into the formula below:
lux = C (f-stop²/shutter (in seconds))/ISO
Exposure Value Calculator:
https://snapheadshots.com/resources/exposure-and-light-calculator
https://www.scantips.com/lights/exposurecalc.html
From that perspective, an exposure stop is a measurement of Exposure and provides a universal linear scale to measure the increase and decrease in light, exposed to the image sensor, due to changes in shutter speed, iso & f-stop.
+-1 stop is a doubling or halving of the amount of light let in when taking a photo.
1 EV is just another way to say one stop of exposure change.
One major use of EV (Exposure Value) is just to measure any change of exposure, where one EV implies a change of one stop of exposure. Like when we compensate our picture in the camera.
If the picture comes out too dark, our manual exposure could correct the next one by directly adjusting one of the three exposure controls (f/stop, shutter speed, or ISO). Or if using camera automation, the camera meter is controlling it, but we might apply +1 EV exposure compensation (or +1 EV flash compensation) to make the result goal brighter, as desired. This use of 1 EV is just another way to say one stop of exposure change.
On a perfect day the difference from sampling the sky vs the sun exposure with diffusing spot meters is about 3.2 exposure difference.
~15.4 EV for the sun
~12.2 EV for the sky
That is as a ballpark. All still influenced by surroundings, accuracy parameters, fov of the sensor…
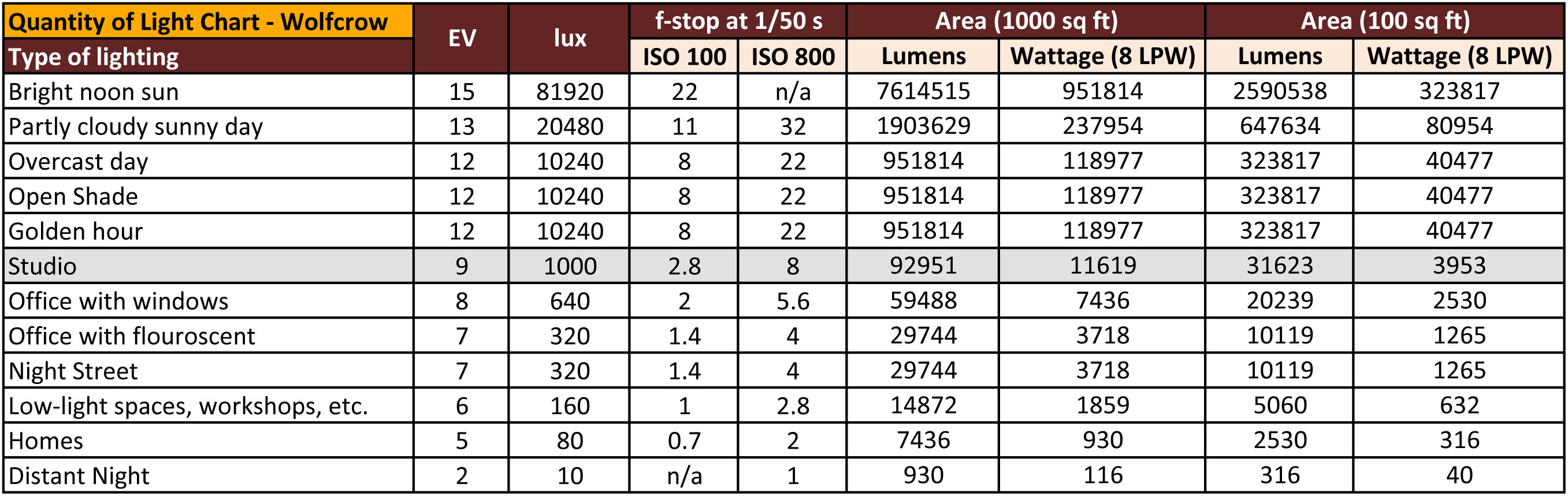
EV calculator
https://www.scantips.com/lights/evchart.html#calc
http://www.fredparker.com/ultexp1.htm
Exposure value is basically used to indicate an interval on the photographic exposure scale, with a difference of 1 EV corresponding to a standard power-of-2 exposure step, also commonly referred to as a “stop”.
https://contrastly.com/a-guide-to-understanding-exposure-value-ev
Retrieving photographic exposure from an image
All you can hope to measure with your camera and some images is the relative reflected luminance. Even if you have the camera settings.
https://en.wikipedia.org/wiki/Relative_luminance
If you REALLY want to know the amount of light in absolute radiometric units, you’re going to need to use some kind of absolute light meter or measured light source to calibrate your camera. For references on how to do this, see: Section 2.5 Obtaining Absolute Radiance from http://www.pauldebevec.com/Research/HDR/debevec-siggraph97.pdf
IF you are still trying to gauge relative brightness, the level of the sun in Nuke can vary, but it should be in the thousands. Ie: between 30,000 and 65,0000 rgb value depending on time of the day, season and atmospherics.
The values for a 12 o’clock sun, with the sun sampled at EV 15.5 (shutter 1/30, ISO 100, F22) is 32.000 RGB max values (or 32,000 pixel luminance).
The thing to keep an eye for is the level of contrast between sunny side/fill side. The terminator should be quite obvious, there can be up to 3 stops difference between fill/key in sunny lit objects.
Note: In Foundry’s Nuke, the software will map 18% gray to whatever your center f/stop is set to in the viewer settings (f/8 by default… change that to EV by following the instructions below).
You can experiment with this by attaching an Exposure node to a Constant set to 0.18, setting your viewer read-out to Spotmeter, and adjusting the stops in the node up and down. You will see that a full stop up or down will give you the respective next value on the aperture scale (f8, f11, f16 etc.).
One stop doubles or halves the amount or light that hits the filmback/ccd, so everything works in powers of 2.
So starting with 0.18 in your constant, you will see that raising it by a stop will give you .36 as a floating point number (in linear space), while your f/stop will be f/11 and so on.
If you set your center stop to 0 (see below) you will get a relative readout in EVs, where EV 0 again equals 18% constant gray.
Note: make sure to set your Nuke read node to ‘raw data’
In other words. Setting the center f-stop to 0 means that in a neutral plate, the middle gray in the macbeth chart will equal to exposure value 0. EV 0 corresponds to an exposure time of 1 sec and an aperture of f/1.0.
To switch Foundry’s Nuke’s SpotMeter to return the EV of an image, click on the main viewport, and then press s, this opens the viewer’s properties. Now set the center f-stop to 0 in there. And the SpotMeter in the viewport will change from aperture and fstops to EV.
If you are trying to gauge the EV from the pixel luminance in the image:
– Setting the center f-stop to 0 means that in a neutral plate, the middle 18% gray will equal to exposure value 0.
– So if EV 0 = 0.18 middle gray in nuke which equal to a pixel luminance of 0.18, doubling that value, doubles the EV.
.18 pixel luminance = 0EV
.36 pixel luminance = 1EV
.72 pixel luminance = 2EV
1.46 pixel luminance = 3EV
…
This is a Geometric Progression function: xn = ar(n-1)
The most basic example of this function is 1,2,4,8,16,32,… The sequence starts at 1 and doubles each time, so
- a=1 (the first term)
- r=2 (the “common ratio” between terms is a doubling)
And we get:
{a, ar, ar2, ar3, … }
= {1, 1×2, 1×22, 1×23, … }
= {1, 2, 4, 8, … }
In this example the function translates to: n = 2(n-1)
You can graph this curve through this expression: x = 2(y-1) :
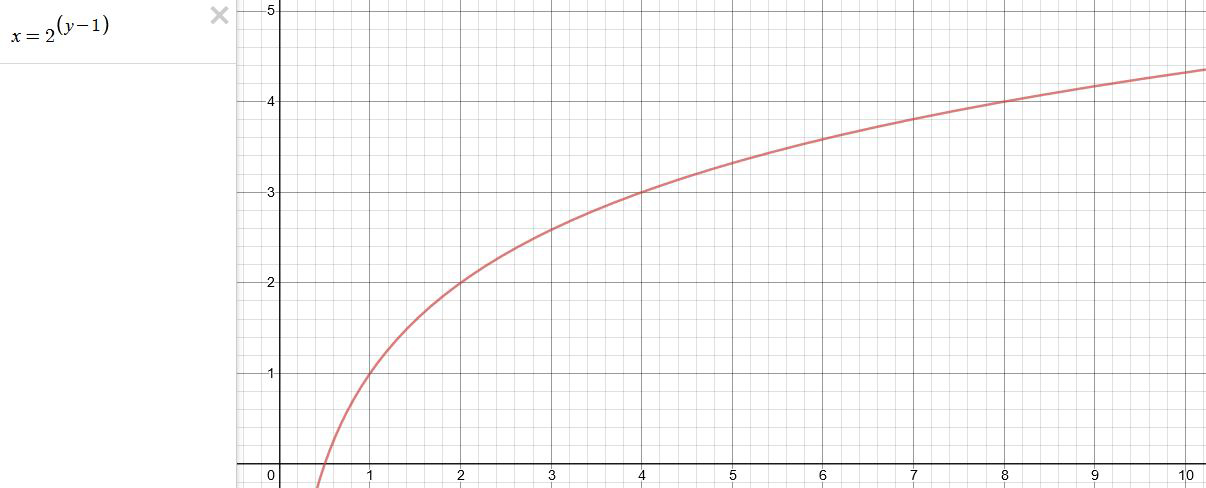
You can go back and forth between the two values through a geometric progression function and a log function:
(Note: in a spreadsheet this is: = POWER(2; cell# -1) and =LOG(cell#, 2)+1) )
| 2(y-1) | log2(x)+1 |
| x | y |
| 1 | 1 |
| 2 | 2 |
| 4 | 3 |
| 8 | 4 |
| 16 | 5 |
| 32 | 6 |
| 64 | 7 |
| 128 | 8 |
| 256 | 9 |
| 512 | 10 |
| 1024 | 11 |
| 2048 | 12 |
| 4096 | 13 |
Translating this into a geometric progression between an image pixel luminance and EV:
| 2(y-2.47393118833241) | log2(x)+2.47393118833241 |
| x = Pixel Luminance | y = EV |
| 0.18 | 0 |
| 0.36 | 1 |
| 0.72 | 2 |
| 1.44 | 3 |
| 2.88 | 4 |
| 5.76 | 5 |
| 11.52 | 6 |
| 23.04 | 7 |
| 46.08 | 8 |
| 92.16 | 9 |
| 184.32 | 10 |
| 368.64 | 11 |
| 737.28 | 12 |
| 1474.56 | 13 |
| 2949.12 | 14 |
| 5898.24 | 15 |
| 11796.48 | 16 |
| 23592.96 | 17 |
| 47185.92 | 18 |
So in very rough terms based on a neutral plate, at an exposure time of 1 sec and an aperture of f/1.0 and a considering a iso 100 constant:
sunny day = ~25000 pixel luminance = ~17 EV
studio flash lamp = ~2000 pixel luminance = ~13.5 EV
It is important to point out that EV is dependent on the film speed (ISO). All above is true only for ISO 100. It is easy to convert to other speeds, though: EV(at ISO 100) == EV(at ISO 200) - 1
Photographic exposure is the amount of light per unit area (the image plane illuminance times the exposure time) reaching a photographic film or electronic image sensor, as determined by shutter speed, lens aperture and scene luminance. Exposure is measured in lux seconds, and can be computed from exposure value (EV) and scene luminance in a specified region.
Lux (lx) is used as a measure of the intensity, as perceived by the human eye, of light that hits or passes through a surface. Lux is an unit of light measurement where the area is also taking in account. In other words, light RECEIVED in a specific area. Which ia a more appropriate data collection mechanism with lights like the sun and the sky, where it is extremely hard to measure the total light emitted. A blue sky alone, without sun, could go into the 45000-70000 lux.
If you dont have any photographic metadata, you could consider using the “sunny 16” rule. Which basically says that whatever ISO film you have, you set an aperture of f/16 and then an exposure of the inverse of the ISO, ie for ISO 100: 1/100
https://www.jeffgeerling.com/blogs/jeff-geerling/converting-between-exposure
It’s better, for determining EV (Exposure Value) or LUX values, to measure the incident light… and you can only do this accurately with a spot/light meter. (You can estimate the reflected light by taking a picture with your camera, and glancing at the exposure at given settings. If the exposure is decent, look at the meter settings you used—ISO, aperture, and shutter speed).
Once you have a reading, you can do two conversions to reach the approximate LUX value. First, you need to convert to an EV (Exposure Value), then to LUX.
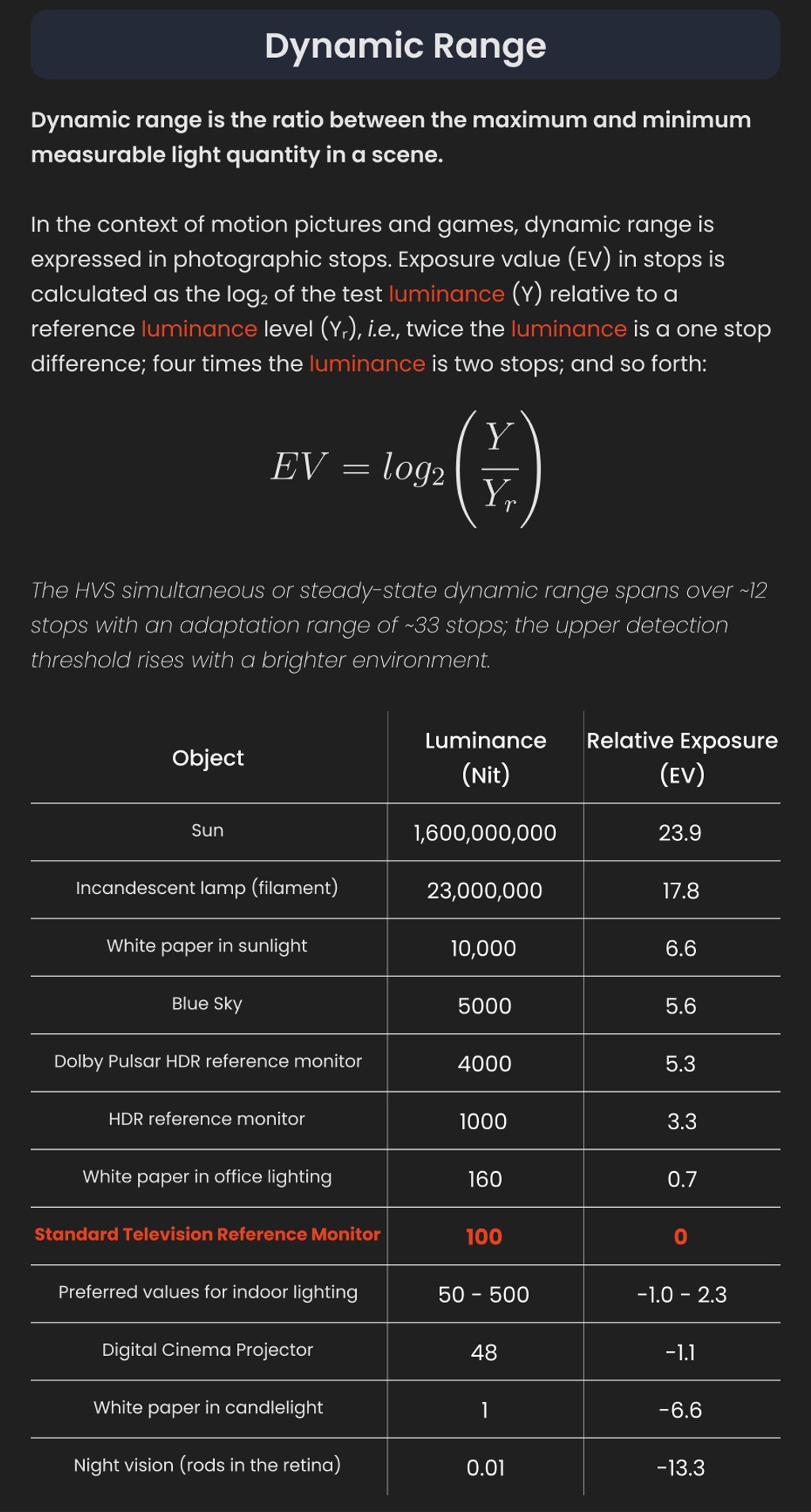
For the first conversion, use your aperture and shutter speed readings, at ISO 100, and get the resulting EV. Use the table below, found under the “EV as an indicator of camera settings” heading in this Wikipedia article:
| EV | f-number | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.0 | 1.4 | 2.0 | 2.8 | 4.0 | 5.6 | 8.0 | 11 | 16 | 22 | 32 | 45 | 64 | |
| −6 | 60 | 2 m | 4 m | 8 m | 16 m | 32 m | 64 m | 128 m | 256 m | 512 m | 1024 m | 2048 m | 4096 m |
| −5 | 30 | 60 | 2 m | 4 m | 8 m | 16 m | 32 m | 64 m | 128 m | 256 m | 512 m | 1024 m | 2048 m |
| −4 | 15 | 30 | 60 | 2 m | 4 m | 8 m | 16 m | 32 m | 64 m | 128 m | 256 m | 512 m | 1024 m |
| −3 | 8 | 15 | 30 | 60 | 2 m | 4 m | 8 m | 16 m | 32 m | 64 m | 128 m | 256 m | 512 m |
| −2 | 4 | 8 | 15 | 30 | 60 | 2 m | 4 m | 8 m | 16 m | 32 m | 64 m | 128 m | 256 m |
| −1 | 2 | 4 | 8 | 15 | 30 | 60 | 2 m | 4 m | 8 m | 16 m | 32 m | 64 m | 128 m |
| 0 | 1 | 2 | 4 | 8 | 15 | 30 | 60 | 2 m | 4 m | 8 m | 16 m | 32 m | 64 m |
| 1 | 1/2 | 1 | 2 | 4 | 8 | 15 | 30 | 60 | 2 m | 4 m | 8 m | 16 m | 32 m |
| 2 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 15 | 30 | 60 | 2 m | 4 m | 8 m | 16 m |
| 3 | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 15 | 30 | 60 | 2 m | 4 m | 8 m |
| 4 | 1/15 | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 15 | 30 | 60 | 2 m | 4 m |
| 5 | 1/30 | 1/15 | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 15 | 30 | 60 | 2 m |
| 6 | 1/60 | 1/30 | 1/15 | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 15 | 30 | 60 |
| 7 | 1/125 | 1/60 | 1/30 | 1/15 | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 15 | 30 |
| 8 | 1/250 | 1/125 | 1/60 | 1/30 | 1/15 | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 15 |
| 9 | 1/500 | 1/250 | 1/125 | 1/60 | 1/30 | 1/15 | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 |
| 10 | 1/1000 | 1/500 | 1/250 | 1/125 | 1/60 | 1/30 | 1/15 | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 |
| 11 | 1/2000 | 1/1000 | 1/500 | 1/250 | 1/125 | 1/60 | 1/30 | 1/15 | 1/8 | 1/4 | 1/2 | 1 | 2 |
| 12 | 1/4000 | 1/2000 | 1/1000 | 1/500 | 1/250 | 1/125 | 1/60 | 1/30 | 1/15 | 1/8 | 1/4 | 1/2 | 1 |
| 13 | 1/8000 | 1/4000 | 1/2000 | 1/1000 | 1/500 | 1/250 | 1/125 | 1/60 | 1/30 | 1/15 | 1/8 | 1/4 | 1/2 |
| 14 | 1/16000 | 1/8000 | 1/4000 | 1/2000 | 1/1000 | 1/500 | 1/250 | 1/125 | 1/60 | 1/30 | 1/15 | 1/8 | 1/4 |
| 15 | 1/32000 | 1/16000 | 1/8000 | 1/4000 | 1/2000 | 1/1000 | 1/500 | 1/250 | 1/125 | 1/60 | 1/30 | 1/15 | 1/8 |
| 16 | 1/32000 | 1/16000 | 1/8000 | 1/4000 | 1/2000 | 1/1000 | 1/500 | 1/250 | 1/125 | 1/60 | 1/30 | 1/15 | |
| 17 | 1/32000 | 1/16000 | 1/8000 | 1/4000 | 1/2000 | 1/1000 | 1/500 | 1/250 | 1/125 | 1/60 | 1/30 | ||
| 18 | 1/32000 | 1/16000 | 1/8000 | 1/4000 | 1/2000 | 1/1000 | 1/500 | 1/250 | 1/125 | 1/60 | |||
| 19 | 1/32000 | 1/16000 | 1/8000 | 1/4000 | 1/2000 | 1/1000 | 1/500 | 1/250 | 1/125 | ||||
| 20 | 1/32000 | 1/16000 | 1/8000 | 1/4000 | 1/2000 | 1/1000 | 1/500 | 1/250 | |||||
| 21 | 1/32000 | 1/16000 | 1/8000 | 1/4000 | 1/2000 | 1/1000 | 1/500 | ||||||
| EV | 1.0 | 1.4 | 2.0 | 2.8 | 4.0 | 5.6 | 8.0 | 11 | 16 | 22 | 32 | 45 | 64 |
| f-number | |||||||||||||
For the second conversion, use this simple EV to LUX converter, and input the value you determined in the first conversion. Zipped here:
In more details, by inspecting an EV to LUX conversion table using a C constant of 250, it’s possible to see a pattern:
EV Lux -1 1.25 -0.5 1.75 0 2.50 0.5 3.50 1 5.00 1.5 7.00 2 10.00 2.5 14.00 3 20.00 3.5 28.00 4 40.00 ...
1 EV is 5 Lux. 2 EV is 10 Lux. 3 EV is 20 Lux. So, it looks logarithmic:
Wikipedia returns the following formula to build a relation between EV and illuminance (lux) at 100 ISO and C constant of 250:
lux = 2.5 * 2(EV)
With the inverse being something like:
EV = log2(lux)-1.3219280949
So in very rough rounded terms, based at a constant of 100 ISO:
sunny day = ~115.000 lux = ~15.5EV lux shadow = ~10.000 lux (~3 stops) = ~12EV overcast = ~3.500 lux = ~10.5EV office light = ~500 lux = ~7.5EV candle = 1 lx = ~-1.5EV
| Lighting condition | EV100 | LUX | Pixel Luminance |
| DAYLIGHT | |||
| Light sand or snow in full or slightly hazy sunlight (distinct shadows)a | 16 | 163840 | 11796.48 |
| Typical scene in full or slightly hazy sunlight (distinct shadows)a, b | 15 | 81920 | 5898.24000000001 |
| Typical scene in hazy sunlight (soft shadows) | 14 | 40960 | 2949.12000000001 |
| Typical scene, cloudy bright (no shadows) | 13 | 20480 | 1474.56 |
| Typical scene, heavy overcast | 12 | 10240 | 737.280000000002 |
| Areas in open shade, clear sunlight | 17 | 327680 | 23592.96 |
| OUTDOOR, NATURAL LIGHT | |||
| Rainbows | |||
| Clear sky background | 15 | 81920 | 5898.24000000001 |
| Cloudy sky background | 14 | 40960 | 2949.12000000001 |
| Sunsets and skylines | |||
| Just before sunset (12-14 range) | 13 | 20480 | 1474.56 |
| At sunset | 12 | 10240 | 737.280000000002 |
| Just after sunset (9-11 range) | 10 | 2560 | 184.32 |
| The Moon,c altitude > 40°altitude | |||
| Full | 15 | 81920 | 5898.24000000001 |
| Gibbous | 14 | 40960 | 2949.12000000001 |
| Quarter | 13 | 20480 | 1474.56 |
| Crescent | 12 | 10240 | 737.280000000002 |
| Blood moon (0-3 range) | 1.5 | 7.07106781186548 | 0.509116882454315 |
| Moonlight, Moon altitude > 40° | |||
| Full (−3 to −2 range) | -2.5 | 0.441941738241592 | 0.031819805153395 |
| Gibbous | -4 | 0.15625 | 0.01125 |
| Quarter | -6 | 0.0390625 | 0.0028125 |
| Aurora borealis and australis | |||
| Bright (−4 to −3 range) | -3.5 | 0.220970869120796 | 0.015909902576697 |
| Medium (−6 to −5 range) | -5.5 | 0.055242717280199 | 0.003977475644174 |
| Milky Way galactic center (−11 to −9 range) | -10 | 0.00244140625 | 0.00017578125 |
| OUTDOOR, ARTIFICIAL LIGHT | |||
| Neon and other bright signs (9–10 range) | 9.5 | 1810.19335983756 | 130.333921908305 |
| Night sports | 9 | 1280 | 92.1600000000002 |
| Fires and burning buildings | 9 | 1280 | 92.1600000000002 |
| Bright street scenes | 8 | 640 | 46.0800000000001 |
| Night street scenes and window displays (7–8 range) | 7.5 | 452.54833995939 | 32.5834804770762 |
| Night vehicle traffic | 5 | 80 | 5.76000000000001 |
| Fairs and amusement parks | 7 | 320 | 23.04 |
| Christmas tree lights (4–5 range) | 4.5 | 56.5685424949238 | 4.07293505963452 |
| Floodlit buildings, monuments, and fountains (3–5 range) | 4 | 40 | 2.88 |
| Distant views of lighted buildings | 2 | 10 | 0.720000000000001 |
| INDOOR, ARTIFICIAL LIGHT | |||
| Galleries (8–11 range) | 9.5 | 1810.19335983756 | 130.333921908305 |
| Sports events, stage shows, and the like (8–9 range) | 8.5 | 905.096679918781 | 65.1669609541523 |
| Circuses, floodlit | 8 | 640 | 46.0800000000001 |
| Ice shows, floodlit | 9 | 1280 | 92.1600000000002 |
| Offices and work areas (7–8 range) | 7.5 | 452.54833995939 | 32.5834804770762 |
| Home interiors (5–7 range) | 6 | 160 | 11.52 |
| Christmas tree lights (4–5 range) | 4.5 | 56.5685424949238 | 4.07293505963452 |
Other useful conversions:
https://www.translatorscafe.com/unit-converter/en-US/illumination
Other charts